|
|
конспекты
занятий по курсу «Теория и реализация языков программирования» Пример для самостоятельного изучения интересующихся |
|
|||||
|
|
|
||||||
|
|
КЗ-грамматики
и примеры на их решение входили в задание и программу контрольных и экзаменов
по курсу со времени его основания в 7.1. Напомним определения формальных грамматик типа 0
и 1 7.1.1.
Грамматики общего вида (грамматики
без ограничений или, по Хомскому, грамматики типа 0). Формальный
вид правил грамматик
Иными
словами на их правила не накладывается никаких ограничений, т.е. одна любая
цепочка из смеси знаков основного и вспомогательного алфавита языка (не
нулевой длины) может заменяться на таким же образом составленную другую, в
том числе нулевой длины, т.е. пустую. 7.1.2.
Несокращающие грамматики (или контекстно-зависимые грамматики (КЗГ) или грамматики типа 1). Англоязычное слово
«контекст» (context) в данном случае
переводится как «окружение» (заменяемого знака). Формальный
вид правил грамматик
То
есть ни одно правило не должно сокращать длину цепочки в ходе вывода.
Единственное уточнение связано со случаем, когда формальный язык содержит
пустую цепочку. В этом случае её разрешается породить непосредственно из
аксиомы (начального «Ничто»), причём знак аксиомы не должен встречаться в
правых частях никакого из правил грамматики (когда он уже успел стать
«чем-то»). 7.2. Пример контекстно-зависимой грамматики На
прошлой встрече студентам было предложено самостоятельно попробовать
построить грамматику для задачи
т.е. порождающей
цепочки a, a4, a9, a16 и т.д. |
|
|||||
|
|
Поэтому занятие началось с рассмотрения решения, предложенного
студентом Александром С., основанного на том известном свойстве квадратов,
что разности их степеней образуют арифметическую прогрессию (4-1 = 3, 9-4 = 5, 16-9 = 7 и т.д.) Решение оказалось правильным (желающие могут попробовать
его воспроизвести), но не является единственным. Для
разнообразия приведём ещё одно решение данной задачи, использующее более
общий подход, который можно применить, к примеру, для порождения цепочек,
длины которых являются кубами положительных целых чисел. Подход
основан на собственно «квадратности» интересующих нас чисел, т.е. того,
что каждое квадратное число представимо наподобие матрицы из n
строк и |
|
|
||||
|
|
n столбцов единичных элементов (в связи с
чем Пифагор и дал название подобным числам - квадратные, а
среди других чисел по тому же принципу отметил треугольные, кубические,
пирамидальные и т.п.). |
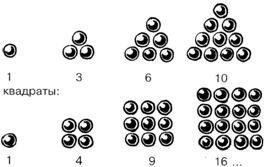
Рис. Треугольные
и квадратные числа по Пифагору |
|
||||
|
|
Для определённости поставим себе конечной целью создать неукорачивающую
грамматику, т.е. такую, в которой ни одна из цепочек в ходе вывода не
становится короче (желательность такого ограничения разъясняется в следующем
параграфе). Итак, порождаем
две группы по n элементов |
|
|||||
|
|
Правила |
Вид получаемой
цепочки |
|
||||
|
|
|
Cn Dn |
|
||||
|
|
|
Cn-1 DCA Dn-1 (A задерживает дальнейшее продвижение C) |
|
||||
|
|
|
(DAn)n Cn (отработали все C) |
|
||||
|
|
|
(Dan)n Cn |
|
||||
|
|
Получили
Но если мы просто дополним грамматику (пока даже не
сдерживая решение неукорачиваемостью) правилами
то
вывод может закончиться в случайный момент времени, в том числе досрочно, и
станет возможным порождение лишних цепочек. Например, Ниже будет приведено решение. Тем, кто настроился получить
наибольшую отдачу от курса, советуем по возможности уделить несколько
мгновений и попытаться самостоятельно осознать задачу и предложить её
решение, а лишь затем сравнить его с нашим (может быть, у вас будет лучше!) * * * Итак, сложность состоит в том, что от знаков C и D необходимо
освободиться, но только тогда, когда они полностью выполнят своё
предназначение. Это противоречивое требование говорит не о нерешаемости
данной задачи, а пока только о том, что она относится к определённому виду
задач, по своему существу упирающихся в некоторое противоречие (что-то должно
и быть и не быть, либо быть одновременно в разных местах или в разное время,
быть сразу холодным и горячим, заряженным и незаряженным и т.д.) Общие
подходы выявления и успешного разрешения противоречий в подобных задачах были
собраны и обобщены более полувека назад (первая статья в В данном случае применяется типовой приём «изменение
состава системы»: необходимо уточнить назначение и состав «действующих лиц» в
правилах грамматики. Выделим для этого самый первый из команды знаков C
(назовём его B) и самый последний из D (обозначим его E). Когда B и E
встретятся, это и будет признаком полного завершения порождения знаков a. На основе подобных соображений до
того единое древнее войско начали разделять на разные полки – передовые,
засечные (заградительные), разведывательные и т.д. – каждые со своими
задачами. Начнём вывод с начала (за S' обозначен новый вспомогательный знак): |
|
|||||
|
|
Правила |
Вид получаемой цепочки |
|
||||
|
|
|
B S'E |
|
||||
|
|
|
B Cn Dn E |
|
||||
|
|
|
B Cn-1 (DA)n CE (C прошло первый раз) |
|
||||
|
|
|
B (DAn)n Cn
E (прошли все C) |
|
||||
|
|
|
BAn
(DAn)n-1 Cn E |
|
||||
|
|
|
An*n B Cn E (ушли
все D) |
|
||||
|
|
|
An*n B E (ушли
все C) |
|
||||
|
|
|
An*n (ушли B и E) |
|
||||
|
|
|
an*n |
|
||||
|
|
Желаемое получили, но какой ценой (для B, C, D и E)?
Прямо-таки сталинские приёмы. Точнее скажем, в военных или иных чрезвычайных
условиях иначе, порой, и нет возможности поступить. А в более мирное время?
Попробуем «соблюдать КЗОТ» и обойтись без сокращений. Снова: |
|
|||||
|
|
Правила |
Вид получаемой цепочки |
|
||||
|
|
|
B S'E |
|
||||
|
|
|
B Cn Dn E |
|
||||
|
|
|
B Cn-1 (DA)n CE (прошло первое C) |
|
||||
|
|
|
B (DAn)n Cn
E (прошли все C) |
|
||||
|
|
|
a2BAn(DAn)n-1CnE |
|
||||
|
|
|
(a2An)n
BCnE (ушли все D) |
|
||||
|
|
|
(a2An)nBEa2n (ушли все C) |
|
||||
|
|
|
an*n+4n+4
= a((n+2)*(n+2)) |
|
||||
|
|
|
an*n+2n
BE a2n |
|
||||
|
|
|
(восполнили
частные решения) |
|
||||
|
|
Итак,
если сокращать нельзя, достраиваем слово до ближайшего подходящего квадрата
(ведь язык – это множество цепочек, а не одна «единственно верная»). В данном случае удобнее достроить слово до a((n+2)*(n+2)), т.к. для достройки
до a((n+1)*(n+1)) нам бы когда-то
потребовалось перевести Некоторые дополнительные подробности решения данной задачи
приведены в [1] (гл. 2). Чуть позже мы увидим в определениях, что в несокращающих
грамматиках допускается переход аксиомы в пустую цепочку (e), если аксиома нигде более не
встречается в правых частях правил (т.е. когда из начального ничего получают
другое ничего). Заметим качественное отличие возможностей последней
грамматики от ранее рассмотренных нами: она обладает своего рода памятью,
т.е. возможностью учёта предыстории и обстоятельств вывода через учёт
окружения заменяемого знака. Для порождения некоторых языков, включая последний
из рассмотренных, эта возможность является существенной. Если бы мы могли
заменять в каждом правиле только по одному знаку, то такой памяти грамматика
была бы лишена. |
|
|||||
|
|
7.3. Задачи. Вы можете попробовать свои силы в построении КЗГ, например,
порождающих следующие языки: А. Б. В. Г. Д. |
|
|||||
|
|
7.4. Сравнительные достоинства и недостатки разных
видов грамматик Из определений
видно, что самыми большими выразительными возможностями и самыми малыми
ограничениями на правила обладают грамматики общего вида. Возникает мысль –
если они «самые мощные», то почему бы не использовать всегда только их? Тем
более и примеры подобного подхода нам широко известны. Если
мы, скажем, упоминаем об управляющей программе для ПЭВМ, то, скорее всего,
подразумеваем Windows, если о
текстовом редакторе для этой системы, то MsOffice. Такой подход сложился у нас в России во многом благодаря
особенностям законодательства и его правоприменения, особенно в 90-е годы. Но
в тех странах, где более строго осуществляется надзор за соблюдением
авторского права (разумеется, не как главная и единственная мера, а как
естественное продолжение поддержки законной предпринимательской деятельности
и вплоть до воспитания и поддержания
хороших привычек населения), где за дополнительные, в т.ч. редко используемые
возможности Ms Word приходится доплачивать заметные суммы, мы
наблюдаем большое разнообразие текстовых редакторов, в т.ч. более простых и,
соответственно, более доступных. Так и
в грамматиках за дополнительные выразительные возможности приходится расплачиваться
большей сложностью и трудоёмкостью работы с ними. Для
самых простых праволинейных грамматик (ПГ) известно множество формальных
алгоритмов для работы с ними, в частности, как перейти от представления
формального языка с помощью ПГ к его представлению в виде регулярного
выражения или конечного автомата и обратно. Соответствующие языки получили название регулярных, а само слово формально означает возможность
осуществить такое преобразование для любого регулярного языка, в частности,
с помощью машины. Множество
формальных алгоритмов известно и для контекстно-свободных
языков, но эти алгоритмы уже более сложные. Наиболее заметно качественное
различие между регулярными и КС-языками при сравнении устройства
соответствующих формальных автоматов: для разбора КС-языков в автомат
пришлось добавить ещё одно «устройство» - магазин (стек). Такие автоматы (они
получили название магазинных) мы рассмотрим в нашем курсе несколько позже. Устройство
соответствующих автоматов для КЗГ и грамматик общего вида
(линейно-ограниченного автомата и его обобщения – машины Тьюринга) ещё более
усложняются, а алгоритмы зачастую удаётся применить только для определённых
частных случаев (каким являются и сами КЗГ для грамматики общего вида).
Весьма сложно и трудоёмко (сравнительно с регулярными и КС-языками)
использовать соответствующие грамматикам общего вида распознаватели и для
программирования. Поэтому
в огромном большинстве современных технических приложений стараются ограничиться
использованием регулярных и КС-языков. Любопытно, что все наиболее
распространённые языки программирования (от Fortran до С++) оказалось возможным осуществить с помощью
подобного подхода. В тоже время известны и такие языки, представить которые с
помощью КСГ невозможно, к примеру, LISP. Для
понимания разницы между грамматиками общего вида и КЗГ обратим внимание на
то, что линейно-ограниченный автомат – это, по существу, машина Тьюринга,
только с ограничением на длину ленты. При создании технических устройств и
программ это различие становится существенным. Заметив,
что КЗГ являются естественной основой многих систем искусственного разума (в
частности, баз знаний и основанных на них экспертных систем) и за их
использованием видится большое будущее, в нашем вводном курсе мы основное
внимание далее уделим более простым КС- и регулярным языкам и приёмам работы
с ними. |
|
|||||
|
|
== Ссылки == [1] Серебряков
В.А. [и др.]. Теория и
реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е
изд). – 294 c. (681.3/ Т33). [2] Курочкин В.М.,
Столяров Л.Н., Сушков Б.Г., Флёров Ю.А. Теория и
реализация языков программирования:
Курс лекций. М.: МФТИ, 1978. [3] Альтшуллер Г.С.
Найти идею. Теория решения изобретательских задач // Новосибирск: Наука (сиб.
отд.), [4] Альтшуллер Г.С. Введение в ТРИЗ. Основные понятия и подходы
// Электр. изд. Фонда Альтшуллера, условно-бесплатное для неком.
распространения. |
|
|||||
|
|
|
||||||
|
|
|
|
|||||