"ТРЯП (конспекты)"

конспекты занятий по курсу «Теория и реализация языков программирования» Занятие 5
(<<<) предыдущий	наверх		следующий (>>>)
5. Условия регулярности языка Строение и некоторые способы задания правильных (регулярных) языков наводит на мысль о возможности создания критерия проверки, с помощью которого можно определить является ли язык правильным. В данном занятии подробно рассматривается вопрос о регулярности конечных языков, а также лемма о накачке для правильных языков (необходимое условие регулярности языка). В конце дана ссылка на материал для изучения теоремы Майхилла-Нероуда, определяющей необходимое и достаточное условие регулярности языка и подробно рассматриваемой на лекции. Поскольку данное занятие является заключительным по правильным языкам, в конце его приводится ряд задач и примеров из данной области.
5.1. Регулярность конечных языков Теорема. Конечный язык всегда регулярен. Действительно, если у нас имеется конечное число (n) слов в языке , то мы всегда можем предложить для этого языка праволинейную грамматику , либо регулярное выражение , либо известным уже нам способом всегда (хотя бы теоретически) сможем построить для него КА. Все эти возможности определённо говорят о регулярности произвольного конечного языка.
5.2. Условия регулярности для бесконечного языка Понятно, что для бесконечного языка применение приведённых в предыдущем разделе приёмов приведёт к началу построения в общем случае бесконечного числа правил грамматики, бесконечного (а не конечного) автомата и т.д., т.е. построения, которое никогда не закончится. Поэтому для таких языков были разработаны свои критерии, помогающие прояснить вопрос о регулярности соответствующего языка. 5.2.1. Лемма Огдена (лемма о накачке, лемма о разрастании) (необходимое условие регулярности бесконечного языка) Эта лемма вытекает из следующих простых соображений. Если у нас есть ДКА, где каждое состояние при исследовании любой из входных цепочек может быть посещено не более одного раза, то понятно, что длина принимаемой цепочки не может превышать числа состояний данного автомата. Например:
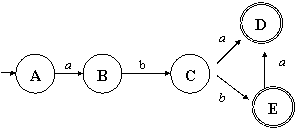
				Этот автомат никогда не примет цепочку длиннее 4 знаков.
Если же длина принимаемой КА цепочки не меньше, чем число состояний ДКА, то очевидно, что какое-то состояние при разборе данной цепочки было посещено повторно, т.е. данный КА имеет хотя бы одно кольцо (круговорот) состояний, т.е. имеет подмножество состояний, передача управления по которым может происходить по кругу. Например:
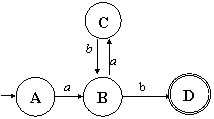
		Этот автомат может принять цепочку неограниченно большой длины.
Наличие такого круговорота отражается и в записи соответствующего РВ: Если переписать это РВ с использованием степени то можно утверждать, что слово для любого будет принадлежать данному РЯ. В более общем виде это наблюдение можно записать так: Если цепочку языка можно представить как причём то это один из признаков того, что данный язык – регулярный. Понятно, что цепочка h не должна быть пустой, иначе получим вырожденный случай, выполняющийся для любого языка. В данном определении не учтено одно обстоятельство. Предваряющая и заключающая цепочки j и y могут быть достаточно длинными, поэтому если возьмём слишком короткое слово, то может так получится, что нам не удастся подобрать соответствующее h даже в регулярном языке (для короткого слова степень его вхождения будет равна нулю). И критерий не сработает. Поэтому полная формулировка Леммы о разрастании говорит о том, что критерий должен выполняться только начиная со всех слов языка не короче некоторого k. Итак: Если для языка L существует величина k, такая, что любое слово из L не короче k можно представить как и выполняется то это является необходимым условием того, что данный язык регулярен.
5.3. Примеры применения леммы о разрастании Пример 5.3.1. Применим данную лемму для языка Если этот язык регулярен, то для достаточно большого k ещё более длинную цепочку можно представить в требуемом леммой виде. Попробуем это сделать, рассмотрев разные возможности выбора цепочки разрастания h для цепочки, к примеру, . 1. Если взять или , то цепочка вида , но , поскольку нарушится соотношение a и b в получаемых словах. 2. По той же причине не выполнится лемма и при выборе или или . 3. Если мы выберем за , то при возведении h в степень большую 1 у нас нарушится порядок букв в слове. Поскольку иначе h подобрать для удовлетворения условия леммы также, очевидно, нельзя, то необходимое условие регулярности для данного языка не выполнено и он не является регулярным. Пример 5.3.2. Применим данную лемму для языка В этом случае для любого допустимого n и любого заранее заданного большого числа k мы можем взять и все слова будут длинной не менее k и принадлежать нашему языку. Т.е. необходимое условие регулярности для этого языка выполнено. В тоже время известно, что данный язык не является регулярным.
Упражнение 5.1. Можно ли утверждать, что за k в вышеприведённой лемме может быть взято число состояний ДКА, задающего исследуемый на регулярность язык (если такой ДКА, разумеется, существует)? Упражнение 5.2. Как вы думаете – можно ли предложить подобную лемму для контекстно-свободных языков? Если да, то в чём будет их отличие? Сможете ли вы её записать?
5.4. Примеры задач на регулярные языки Пример 5.4.1. Построить ДКА для языка {x {0, 1}* : на каждом кратном двум месте цепочки которого (1, 3, 5, …) стоит знак 0 (нумерация знаков начинается с 1), а \|x\|₁ – чётно}. Самые короткие цепочки из данного языка такие: , 0, 00, 000, 0000, 0101 и т.д. Не будем торопиться переходить к решению этой, в общем-то, простой задачи, а сначала постараемся разобрать её условие, понять, что оно может нам подсказать о будущих свойствах ДКА или ПГ, которые соответствуют данному языку. Заметим, что в условии задачи указаны два ограничения, одно из которых касается нулей, второе – единиц. По нулям имеем следующие состояния: А – мы на кратном двум месте цепочки (начиная с 1-го), здесь должен стоять 0 B – мы на некратном двум месте, здесь может стоять как 0, так и 1.
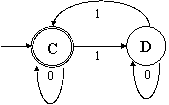
Рис. 5.4. ДКА для подмножества искомого языка {x {0, 1}* : на каждом кратном двум месте цепочки которого (1, 3, 5, …) стоит знак 0 (нумерация знаков начинается с 1).
По единицам состояния таковы: С – в данное время принято (порождено) чётное число единиц, это состояние может быть завершающим. D - \|x\|₁ – нечётно, состояние не может быть завершающим.
Рис. 5.5. ДКА для подмножества искомого языка {x {0, 1}* : \|x\|₁ – чётно).
Учёт каждого из этих ограничений по отдельности требует самое меньшее двух состояний. Поскольку ни одно из ограничений не зависит от другого, то комбинаторика подсказывает, что искомый ДКА должен содержать хотя бы 2 × 2 = 4 состояния. Попробуем их перечислить: А - кратное двум место цепочки, \|x\|₁ – чётно. Состояние завершающее. B - некратное двум место цепочки, \|x\|₁ – чётно. Состояние завершающее С - кратное двум место цепочки, \|x\|₁ – нечётно. Состояние не завершающее D - некратное двум место цепочки, \|x\|₁ – нечётно. Состояние не завершающее
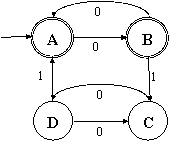
Рис. 5.6. ДКА – итог перемножения двух частных ДКА - подмножеств искомого языка.
Задача 5.2. Построить ДКА для языка {x {0, 1}* : на каждом кратном трём месте цепочки которого (1, 4, 7, …) стоит знак 0 (нумерация знаков начинается с 1), а \|x\|₁ – нечётно}. Исследовать полученный ДКА на минимальность состояний.
Совет. Познакомьтесь с более кратким математическим описанием соответствующих алгоритмов в пособии [1] и введёнными при этом понятиями и обозначениями. == Ссылки == [1] Серебряков В.А. [и др.]. Теория и реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е изд). – 294 c. (681.3/ Т33). [2] Теорема Майхилла-Нероуда (о необходимых и достаточных условиях регулярности языка). (заметки лектора). [3] Tom Henzinger. Lecture 7. Mayhill-Nerode Theorem. 2003. [4] CSE396. Notes to Mayhill-Nerode Theorem. Spring, 2010.
(<<<) предыдущий	наверх		следующий (>>>)