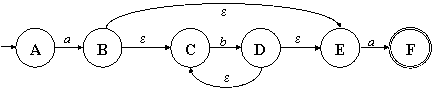конспекты занятий по курсу

 «Теория и реализация языков программирования»

 

Занятие 3

 

 

 

(<<<) предыдущий

наверх

следующий (>>>)

 

 

3. Регулярные языки (продолжение)

3.1. Определённые и неопределённые КА

На функции переходов КА могут быть наложены дополнительные ограничения, связанные с однозначностью (определённостью) перехода из любого заданного состояния КА по данному входному знаку или пустой цепочке. Указанные ограничения не снижают выразительную силу (т.е. возможности по описанию регулярных языков), однако соответствующие КА имеют разные «потребительские» свойства.

Суть различия в том, что в определённых автоматах (deterministic automaton, ДКА) мы можем без возвратов определить допустимость заданной входной цепочки при её разборе, поскольку каждый переход при этом разборе однозначно определён.

Если же у нас неопределённый (nondeterministic) КА (НКА), то выбрав в ходе разбора движение по той или иной развилке управления и не достигнув условия допуска цепочки, мы не можем быть вполне уверенными в том, что если бы мы не пошли по другому возможному пути, то не смогли бы допустить цепочку.

На деле это приводит к тому, что как в самих НКА, так и в тех программных распознавателях, которые строятся по НКА, вынуждены перебирать все возможные пути разбора для недопустимой цепочки, прежде чем уверенно вынести решение о её не принадлежности к заданному языку.

Более формально определение ДКА звучит так:

Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:

 (1)   для любого  и

 (2)   содержит не более одного элемента для любых  и

* * *

Какой из видов представления КА лучше – вопрос не без лукавства (по крайней мере, пока не указано значимое окружение (context) задачи).

Задача на размышление. Диалектика подсказывает, что в любом явлении неразрывно, в единое целое, связаны его различные стороны. При заданном подходе (точке зрения) одни из этих сторон признаются положительными, другие отрицательными. При смене точки зрения соответствующие «этикетки» могут поменяться вплоть до противоположных.

Вопрос в том, существуют ли обстоятельства, при которых НКА могут быть более предпочтительными, чем ДКА? Постарайтесь обосновать свой ответ.

Ответить вам на этот вопрос сразу, возможно, будет затруднительно. Но это и не требуется. Он задаётся именно здесь, до изложения последующих алгоритмов, связанных с ДКА и НКА, именно потому, что подсказки к ответу, которые вы можете приметить при изучении этих алгоритмов, обычно куда быстрее замечаются людьми, чем если бы данная задача была поставлена после и «в отрыве» от собственно содержательного изучения (это один из итогов весьма основательных исследований т. н. когнитивной (cognitive – познавательный) психологии, деятельно проводящихся в мире с 60-х годов ХХ в.)

 

 

 

3.2. Алгоритм перехода РВ ® НКА

Данный алгоритм подробно описан в выложенном в сети пособии [1] (с. 54-56) и, на наш взгляд, никаких сложностей для восприятия не представляет. Единственное, что хотелось бы уточнить: при его применении многих учащихся «подмывает» стремление сразу, в ходе построения, «улучшить» получаемый автомат. Действительно, так вроде бы много явно избыточных переходов по пустой цепочке! Но доказанный алгоритм не содержит случайных действий и при невнимательном упрощении получаемого автомата он легко и незаметно может превратиться в неравнозначный искомому. Особенно осторожно приходится быть с итерацией.

 

 

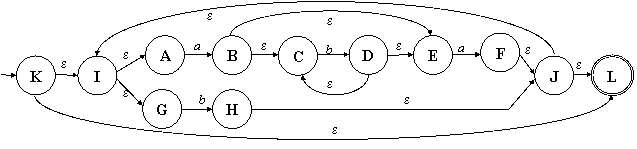
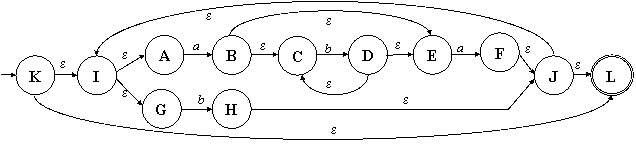
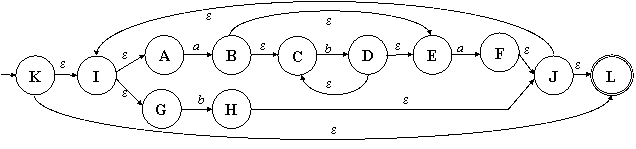
Пример 3.1.  для языка

Из прошлого занятия мы знаем, что ему соответствует РВ

(ab*a | b)*

Перейдём от него пошагово, слева направо, по алгоритму к НКА.

Сначала будем приводить диаграмму состояний соответствующего НКА, а снизу – ту часть РВ, которой он соответствует.

 

 

 

 

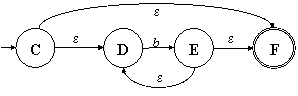
Рис. 3.1. Полученный по алгоритму НКА, соответствующий РВ (a)

 

 

 

 

 

 

 


Рис. 3.2. НКА для РВ (b*)

 

 

 

 

 

 

 


Рис. 3.3. НКА для РВ (ab*a)

 

 

 

 

 

 

 

 


Рис. 3.4. НКА для РВ (ab*a | b)

 

 

 

 

 

 

 

 

Рис. 3.5. Полученный по алгоритму итоговый НКА, соответствующий РВ (ab*a | b)*

 

 

 

 3.3. Алгоритм перехода НКА ® ДКА

Для «уплотнения» полученного НКА применяют алгоритм перехода НКА ® ДКА, основанный на  том наблюдении, что связанные переходами по пустой цепочке состояния НКА, по сути, являются одним и тем же состоянием соответствующего ДКА. Остаётся только собрать такие состояния в новые группы, проставить между ними переходы по непустым цепочкам и получится искомый автомат.

Этот алгоритм также подробно описан в [1] (с. 57-58).

 

 

 

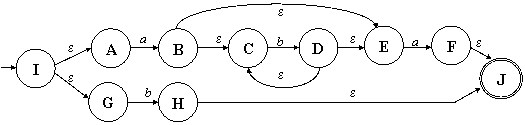
Пример 3.2.  для языка

Замысел алгоритма прост и, разве что возникает вопрос с какого состояния исходного НКА начать. В данной задаче это удобно сделать с начального состояния.

1. Определим совокупность состояний НКА, в которые можно попасть по  из его начального состояния. Это состояния

K, I, A, G, L

Новое состояние ДКА, пока алгоритм не завершился, удобно назвать как их перечень
(K-I-A-G-L), а только потом переименовать более кратко. Назовём этот перечень состояний текущим. Если полученное состояние ДКА нам ещё не было известно, запоминаем его.

2. Определяем совокупность состояний НКА, в которые можно попасть по каждому непустому знаку основного алфавита из текущего перечня состояний НКА.

По знаку (а) мы можем попасть:

 

 

 

 

 

 

 

 

 

из K, I и A – в B (а оттуда по  – в C и E). Из G и L по (а) никуда попасть не можем.

То есть  ( K-I-A-G-L, a) = B-C-E.

По знаку (b) мы можем попасть из K-I-A-G-L в состояние H и связанные с ним по , т.е. в

H-J-A-G

То есть  ( K-I-A-G-L, b) = H-J-I-A-G-L.

Оба полученных нами перечня состояний ранее нам не встречались. Запоминаем их, последовательно делаем их текущими и определяем, куда из них можно попасть по каждому из основных знаков алфавита КА (применяем к каждому из них п. 2).

Пока удаётся выявлять новые состояния ДКА, продолжаем:

Переходы из B-C-E :

 

 

 

 

 

 

 

 

 

 (B-C-E, a) = F-J-L-I-A-G

 (B-C-E, b) = D-E. Оба состояния нам ранее не встречались, запоминаем их.

 

Переходы из  H-J-I-A-G-L :

 (H-J-I-A-G-L, a) = B-C-E

 (H-J-I-A-G-L, b) =  H-J-I-A-G-L

 

Переходы из F-J-L-I-A-G :

 

 

 

 

 

 

 

 

 

 (F-J-L-I-A-G, a) = B-C-E

 (F-J-L-I-A-G, b) = H-J-I-A-G-L

 

Переходы из  D-E :

 (D-E, a) = F-J-L-I-A-G

 (D-E, b) = D-E

Все полученные состояния соответствующего ДКА и переходы между ними нами исследованы, поэтому останавливаемся:  алгоритм завершён.

Для удобства работы с новым ДКА переобозначим его состояния более кратко, например:

 

 

Рабочие обозначения состояний ДКА

Более краткие обозначения

 

 

 ( K-I-A-G-L, a) = B-C-E

 ( K-I-A-G-L, b) = H-J-I-A-G-L

 (B-C-E, a) = F-J-L-I-A-G

 (B-C-E, b) = D-E

 (H-J-I-A-G-L, a) = B-C-E

 (H-J-I-A-G-L, b) =. H-J-I-A-G-L

 (F-J-L-I-A-G, a) = B-C-E

 (F-J-L-I-A-G, b) =. H-J-I-A-G-L

 (D-E, a) = F-J-L-I-A-G

 (D-E, b) =.D-E

 (A, a) = B

 (A, b) = C

 (B, a) = D

 (B, b) = E

 (C, a) = B

 (C, b) = C

 (D, a) = B

 (D, b) = C

 (E, a) = D

 (E, b) = E

 

 

Заметим, что те состояния ДКА, в состав которых входят заключительные состояния НКА (в нашем НКА это состояние L), также являются заключительными. То состояние ДКА, в которое входит начальное состояние НКА (у нас – К) – начальное. Поэтому, в новых обозначениях, заключительными для ДКА являются состояния A, C и D, а начальным – А.

 

 

 

 

 

 

 

 

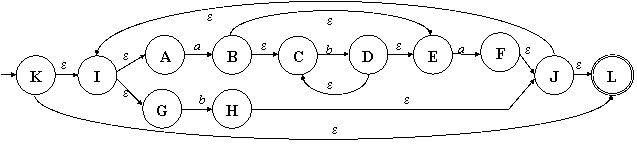
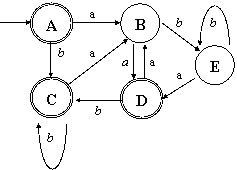
Рис. 3.6. ДКА, полученный по алгоритму из НКА, соответствующий РВ (ab*a | b)*

Любопытно, что полученный КА имеет 5 состояний, хотя мы знаем, что можно было бы обойтись и двумя. Для минимизации конечных автоматов разработан свой алгоритм, к которому мы вернёмся чуть позже, а пока рассмотрим прямой переход из РВ в ДКА.

 

 

4.3. Алгоритм перехода РВ  ДКА

Известен алгоритм прямого перехода из РВ в ДКА, также приведённый в [1]. В силу лаконичности описания некоторых действий алгоритма, его понимание встречает сложности у части учащихся. Поэтому приведём подробный пример его применения для того же РВ (ab*a | b)*.

4.3.1. Вначале пополняют РВ, иначе говоря, к концу РВ приписывают не входящий в Т особый знак, по которому однозначно можно определить завершение выражения. В пособии для этой цели обычно используется знак #. После этого всем знакам из основного алфавита РВ, а также пополненному знаку, приписывают порядковые номера их упоминания в РВ.

Для нашего случая:

Необходимость такой нумерации связана с тем, что один и тот же знак (из Т) может несколько раз встречаться в одном и том же РВ и необходимостью точной ссылки на определённое вхождение данного знака в данном месте РВ. Так, b встречается в нашем РВ как на втором, так и на четвёртом месте, но если мы назовём порядковый номер, например, 4, то однозначно укажем какое именно вхождение данного знака в РВ имеется в виду.

4.3.2. Далее полезно построить дерево, соответствующее данному РВ. Заметим, что при определённом опыте использования алгоритма этот шаг можно и опустить, но наглядность дерева заметно облегчает освоение алгоритма и число возможных неточностей при его применении.

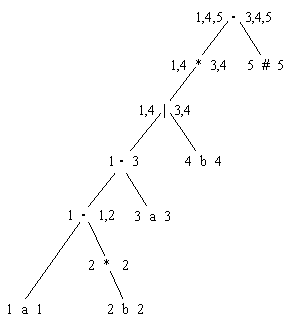
Напомним, что дерево строится по РВ слева направо, а каждый знак из Т в порядке следования его в РВ и каждое действие (объединение, конкатенация, итерация) отмечается на нём отдельной вершиной. Получившееся дерево представлено на рис. 4.7.

Здесь слева от каждой вершины и узла дерева проставлены номера мест знаков в РВ, с которых может начинаться соответствующая данному участку дерева подцепочка в РВ, а справа – номера мест (position), на которые она может окончиться.

Для отдельного знака (вершины дерева) соответствующие значения совпадают с номером знака в РВ. Для узлов – согласно свойствам соответствующих операций. В пособии вычисление этих значений приведено с привлечением функций firstpos () и lastpos (), а также nullable (), учитывающей вероятность возникновения пустой цепочки при использовании итерации в РВ.

Например, узел 1 × 1,2, которому в РВ соответствует подвыражение ab*, может начинаться только со знака «а» (1-й номер в РВ), а заканчиваться либо им же (когда b* включает пустую цепочку), либо на «b» (2-й номер в РВ).

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 3.7. Дерево для пополненного регулярного выражения (ab*a | b)*#

4.3.3. Перед переходом к собственно построению ДКА остаётся вычислить значение ещё одной функции followpos (), определяющей множество мест в РВ, в которые мы можем попасть после данного знака.

Эта функция вычисляется за один обход дерева снизу-вверх для потомков операций конкатенация и итерация (операция «объединение» на значение данной функции не влияет).

По итерации. Пусть n – внутренний узел с операцией * (итерация), u – его потомок. Тогда для каждого номера i, входящего в lastpos(u), добавляем к множеству значений followpos(i) множество firstpos(u).

По конкатенации. Пусть n – внутренний узел с операцией × (конкатенация), u и v – его потомки. Тогда для каждого номера i, входящего в lastpos(u), добавляем к множеству значений followpos(i) множество firstpos(v).

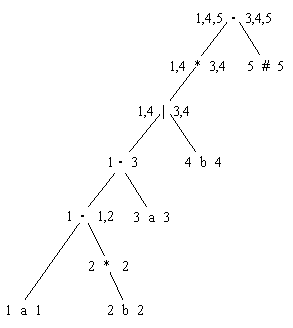
Для нашего примера (приведём для удобство само дерево здесь ещё раз)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Значение функции followpos () для данного дерева приведены ниже.

 

 

 

i

followpos (i)

 

 

 

 

1

2

3

4

2, 3

2, 3

1, 4, 5

1, 4, 5

 

 

 

Так, для вершины (1 . 1,2)  lastpos (1) = 1, а firstpos() от вершины (2 * 2) – 2 (значение это нам предварительно пришлось вычислить зная lastpos (2) = 2, и firstpos(2) = 2).

Следовательно, followpos (1) включает значение 2.

Переходим к вершине (1 . 3). lastpos () от её левого потомка = (1,2), а firstpos() от её правого потомка = 3. Поэтому к значениям функции как followpos (1), так и followpos (2) добавляется значение 3.

Для вершины (2 * 2)   lastpos (2) = 2, и firstpos(2) = 2, поэтому к followpos (2) добавляется значение 2. И т.д.

4.3.4. Строим ДКА

Начальному состоянию будущего ДКА у нас соответствует значение функции firstpos () для корня полученного дерева. Построение ДКА начинаем именно с него.

Итак firstpos () для корня = {1, 4, 5}. Обозначим это состояние как А. Снизу номеров можно для удобства подписать знаки, которые соответствуют указанным номерам в РВ.

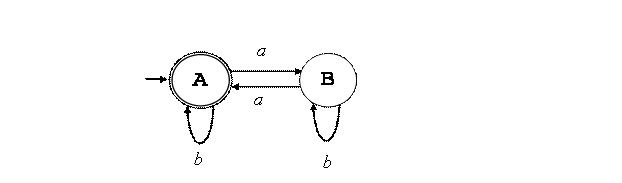
Далее для текущего состояния поочерёдно для каждого знака из Т выбираем все номера, которые соответствуют этому знаку, находим объединение значений followpos () для этих номеров и оно даёт перечень номеров состояния ДКА, в которое мы попадаем по данному знаку.

Так, для «a» в А у нас только один номер – 1. Значение followpos (1) = {2, 3}. Это и будет нашим новым состоянием, которое логично обозначить как B.

Для «b» в А у нас также единственный номер – 4. Значение followpos (4) = {1, 4, 5}, т.е. это уже знакомое нам состояние А.

Подобным образом исследуем состояние B и определяем из него переходы по «a» и «b». Больше состояний в ходе работы алгоритма не появилось, он завершён.

Признаком завершающего состояния в полученном ДКА является наличие в нём номера, соответствующего «#». У нас это состояние А, номеру 5 в котором соответствует # в исходном РВ.

 

 

 

 

Обозначения состояний

Переходы

по «a»

Переходы

по «b»

 

 

 

 

 

B

A

 

 

 

 

 

A

B

 

 

 

 

Любопытно, что данный алгоритм сразу дал минимальный ДКА для исходного РВ.

 

 

 

 

 

Совет. Познакомьтесь с более кратким математическим описанием соответствующих алгоритмов в пособии [1] и введёнными при этом понятиями и обозначениями.

 

== Ссылки ==

[1] Серебряков В.А. [и др.]. Теория и реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е изд). – 294 c. (681.3/ Т33).

 

 

 

 

(<<<) предыдущий

наверх

следующий (>>>)