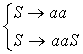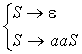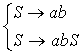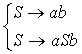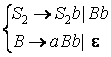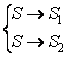|
|
конспекты
занятий по курсу «Теория и
реализация языков программирования» Занятие 1 |
|
||||
|
|
|
|
||||
|
|
1. О содержании и целях наших занятий Сначала
несколько слов о названии, содержании и происхождении нашего предмета, чтобы мы
более точно представляли, чем нам предстоит заниматься. По сути, наши
занятия включают: o начала теории формальных языков – математической
дисциплины, которую
можно приложить в самых разных областях деятельности от
исследования естественных языков (современных, ушедших и даже будущих),
проигрывания итогов деятельности тех или иных сообществ в зависимости от
принятых в них (на бумаге и на деле) уставов поведения до просчитывания
близких и отдалённых последствий генной инженерии (о последнем писали ещё А.Ахо
и Дж.Ульман в предисловии к своей книге [1], рус. перевод o основы приложения упомянутой математической теории в одной из весьма узких и своеобразных технических областей,
а именно создания
быстрых, надёжных и недорогих компиляторов. С этой задачей также
тесно связанны задачи разработки новых формальных языков, которые, с одной
стороны, достаточно мощны и выразительны для описания прикладной области, с
другой – естественно допускают создание компиляторов с указанными выше
свойствами. Эти задачи изучаются преимущественно в курсе ТРЯП. o основы приложения
упомянутой математической теории для «автоматного программирования», т.е.
выявление тех частей программы, которые естественно могут быть представлены
как система формальных автоматов, и воплощение этого представления.
Считается, что при грамотном выполнении подобных действий улучшается
понимаемость и сопровождаемость программы, повышается её надёжность,
облегчаются и более естественным образом выполняются необходимые изменения и
т.п. Эти задачи изучались преимущественно в курсе по выбору «Автоматное
программирование» (в н.в. не читается). Первая,
теоретическая, часть нашего направления в своё время возникла из разбора
(исследования) устройства естественных языков в попытке научиться понимать
смысл предложений на них, используя только формальные (машинные) подходы.
Очевидная цель – построить системы автоматизированного перевода с одного
естественного языка на другой. Соответствующая теория поэтому получила
название структурной лингвистики. В
России начало подобных работ тесно связано с именем выдающегося математика Алексея Андреевича Ляпунова
(8.10.1911 - 23.06.1973). Неоднозначность естественных языков, необходимость
использования для приемлемого понимания предложения определённой предыстории
и привходящих обстоятельств (языкового и смыслового окружения)
высказывания, зачастую огромного числа
сведений, составляющих мировосприятие пишущего и его представление о
мировосприятии и миропонимании читающего, не позволили за прошедшие 70 лет
вполне решить эту задачу для сколько-нибудь сложных текстов на естественных
языках. Но
постановка вопроса о том, какими свойствами должны обладать языки, чтобы их
можно было успешно распознавать, истолковывать, переводить на другие языки,
привела к созданию теории, а затем и разработке многих сотен и тысяч самых
разнообразных формальных языков – от широко известных языков программирования
до входных языков САПР, новых подходов к созданию интегральных схем,
обработке поисковых запросов для интернет и описания самих сетевых страниц,
формальных языков описания и разметки документов и т.д. Эта
теория, в соответствии с изменившимся предметом исследования, получила и
новое название – Теория формальных
языков и автоматов (как распознавателей для цепочек из данных языков). А её
воплощение (realization – англ.) для
одного из востребованных приложений – создания компиляторов – соответственно,
реализацией языков программирования. Джон
Хопкрофт (Joan Hopcroft) – учёный и
автор ряда известных учебников по данному и близким направлениям, совершенно
справедливо говорит в предисловии к [2], что теория формальных языков и автоматов входит в своего
рода ядро информатики, что без изучения и понимания её ныне сложно
представить профессионала в области высоких технологий в программировании. 2. Эволюция преподавания ТРЯП и учебные
пособия по данному направлению В
передовых технических вузах соответствующие курсы появились уже более 40 лет
назад: в МФТИ первое пособие по ТРЯП ([3]) было издано уже в В
связи с широким распространением программирования как профессии, со временем
и у нас, и за рубежом такие курсы стремились сделать более доступными,
оставлять в них только самое необходимое для программирования.
Соответствующие предметы уже стали читаться, начиная с младших курсов, -
сначала на факультетах прикладной математики большинства технических вузов, а
затем и на целом ряде иных технических специальностей. А в начале 2000-х
годов Александром Шенем было подготовлено и первое пособие по
программированию, включающее основы теории и некоторые задачи по формальным
языкам и грамматикам, для учащихся средних школ с углублённым изучением
математики. Данное пособие выдержало несколько бумажных изданий и н.в.
доступно и в электронном виде на сетевой странице МЦНМО (Московский центр
непрерывного математического образования), см. [4].
В нём весьма удачно разъяснён ряд вопросов по формальным языкам и
трансляциям. Дальше
проглядывают уже детские сказки на основе ТРЯП, но будет ли это новым? Если
вспомнить многие настоящие народные (русские, немецкие, татарские…) сказки,
поговорки, пословицы, которые явно связывают определённые правила поведения
(своего рода грамматику плетения узоров жизни) главных действующих лиц с тем,
что с ними происходит, то здесь подходы наших предков остаётся разве что
продолжать и пересказывать для изменившихся условий и обстоятельств жизни
народа. Ныне
знание основ ТРЯП по праву считается основополагающей составляющей подготовки
грамотного профессионала, тем более руководителя разработок сложных
программных систем в области передовых информационных технологий. Теория
и реализация языков программирования в 70-х и 80-х годах прошлого столетия
продолжала быстро развиваться, однако почти 20 лет с 3. Что такое формальный язык и как он
может быть определён. Алфавит
– это конечное множество некоторых знаков. Под формальным языком понимается
множество цепочек, составленных из знаков заданного алфавита и
удовлетворяющих указанным при определении языка ограничениям. Например, язык
из всех цепочек на основе алфавита {a}, таких, что
число букв «а» - чётно, т.е. a2, a4, a6 и т.п. (степенью обозначается число повторений
соответствующего знака (или цепочки)). a0 представляет собой пустую цепочку (обычно
обозначается греческой буквой e). Конечные
языки, т.е. состоящие из конечного множества цепочек, по крайней мере,
теоретически, могут быть определены простым перечислением всех цепочек,
которые в них входят. Для определения целого ряда
семейств востребованных бесконечных
языков оказалось возможным
использовать конечные средства, из
которых наибольшее признание и употребление получили следующие: А. Формальные грамматики, которые
определяют, как породить из начального слова все цепочки (наборы знаков),
принадлежащие заданному языку, и только их. Б. Регулярные выражения (над алфавитом
языка) на основе которых, например, строятся шаблоны выделения групп файлов (например,
*.htm) в командных оболочках ПЭВМ (Norton Commander, Total commander и т.п.), определяются и
преобразовываются поисковые запросы в Internet и т.п. В. Формальные автоматы (конечные, магазинные,
линейно-ограниченные, машины Тьюринга и др.), на вход которых подаётся
цепочка, а на выходе они должны дать ответ - принадлежит ли она языку. 4. Формальные грамматики – определение и
примеры. Пример 1.1. Грамматика для
построения всех цепочек языка на основе алфавита {a}, таких, что число букв «а» положительно и чётно, т.е. a2, a4, a6, …
|
|
||||
|
|
|
|
||||
|
|
Вывод
любой цепочки начинается из начального знака (или аксиомы) грамматики S и осуществляется
заменой S в соответствии с указанными правилами
порождения (цепочка в левой части правила заменяется на цепочку в правой
части). Если имеется несколько подходящих правил, одно из них выбирается
произвольным образом (последовательность их указания в грамматике на это не
влияет). Если заменять уже нечего, вывод останавливается. Так,
если к начальному знаку S мы сразу применим
первое правило
Ни в
одной левой части правил ни знака «а»,
ни цепочки «аа»
не указано, поэтому вывод оказывается закончен. Если
мы начнём вывод со второго правила, то он окажется более длинным и завершится
сразу, когда очередной раз вместо второго правила мы воспользуемся первым:
|
|
||||
|
|
|
|
||||
|
|
После
знакомства с примерами приведём формальные определения. Определение. формальная грамматика G – это математическая сущность на основе
четырёх составляющих: {T, N, P, S}, где T – алфавит
основных знаков языка (из которых собственно строятся его цепочки), N – алфавит
вспомогательных знаков языка (своего рода «строительные леса» грамматики,
которые должны быть убраны при завершении вывода). Начальный знак (аксиома)
грамматики также является вспомогательным. P – совокупность правил порождения
(вывода) цепочек, S – начальный
знак (аксиома) вывода. Пример 1.2. Если из условия
предыдущего примера убрать требование положительности длины цепочки, то в
язык должна быть включена пустая цепочка e (a0), соответственно изменятся и
правила грамматики: |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
Приписывание
пустой цепочки в любом месте цепочки из значащих символов равнозначно её
отсутствию, т.о. вывод по этой грамматике будет выглядеть как
|
|
||||
|
|
|
|
||||
|
|
Отметим,
что если в ходе вывода в цепочке остался хотя бы один вспомогательный знак,
то такой вывод считается незавершённым, а соответствующая цепочка – (ещё или уже)
не принадлежащей языку, порождаемому данной грамматикой. Обычным для
грамматики является случай, когда какие-то выводы могут попадать в «тупик»,
когда ещё остались вспомогательные знаки, а заменить их уже невозможно. Это
говорит только о том, что данная последовательность применения правил не
описывает значащих цепочек языка. Принятые обозначения. Поскольку
основные и вспомогательные знаки грамматики используются заметно различным
образом, то удобно и обозначать их по-разному: Отдельные знаки из основного алфавита языка обозначаются строчными латинскими буквами из начала латинского алфавита ( Отдельные
вспомогательные знаки – заглавными буквами из начала
латинского алфавита ( Для обозначения цепочек из основных и
вспомогательных знаков используются, соответственно, строчные и заглавные
латинские буквы ближе к концу
латинского алфавита. Если нам не требуется различать основные и вспомогательные знаки, то
используются греческий алфавит (начало
алфавита – для отдельных знаков, конец – для обозначения цепочек). В
учебных примерах из одной записи правил грамматики с учётом принятых
обозначений обычно понятно, каковы алфавиты основных и вспомогательных знаков
(или их используемые подмножества, что, по сути, тоже самое), а также какой
знак является начальным, поэтому их отдельно не указывают. Так обычно будем
поступать и мы. При
обозначении правил грамматик в машинном виде (в системах автоматизации
программирования и т.д.), разумеется, используются свои обозначения и
соглашения. Например, в левой части первого из указанных правил грамматики
обязательно указывается её начальный знак (аксиома), греческие знаки
становится использовать не удобно и т.д. С подобными соглашениями вы при
необходимости сможете познакомиться по соответствующим руководствам
программиста. Грамматики
можно различать по самым разным признакам. Одним из самых существенных с
точки зрения наших занятий являются выразительные возможности грамматики,
т.е. их возможности порождать те или иные известные языки. Как мы увидим
далее, эти возможности тесно связаны с ограничениями на вид правил
грамматики. Перед
определениями рассмотрим несколько примеров. |
|
||||
|
|
Пример 1.3. Грамматика
|
|
||||
|
|
|
|
||||
|
|
очевидно,
порождает цепочки вида |
|
||||
|
|
Для
порождения цепочек из языка
|
|
||||
|
|
|
|
||||
|
|
При
введении дополнительных ограничений {anbm| n>m>0} получим: |
|
|
|||
|
|
|
|
||||
|
|
Проверим
себя, что при самом коротком выводе
|
|
||||
|
|
|
|
||||
|
|
мы получим
цепочку, удовлетворяющую ограничениям задачи. Здесь
А – ещё один
вспомогательный знак в дополнение к начальному. По необходимости и для нашего
удобства мы можем использовать любое наперёд заданное конечное число таких
вспомогательных знаков. |
|
||||
|
|
Пример 1.4. Задание
построить грамматику для языка
Ведь
мы уже поняли, что грамматика – это средство что-то построить, дополнить, а не
«отнять», а здесь требуется построить все цепочки за исключением заданных.
Легко увидеть, что указанное противоречие снимается преобразованием условия
задачи к созидательным целям, запись чего, однако, оказывается более длинной:
Правомочность подобного преобразования становится
понятным, если мы вспомним, что формальные языки – это множества цепочек и,
следовательно, с ними можно работать, как и с любыми множествами, т.е.
находить объединение,
пересечение языков, их дополнение и т.д. Запишем частные грамматики для каждого из двух случаев, а
затем объединим их в одну: |
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
Заметим, что
|
|
||||
|
|
а сами При
воплощении решения для каждого из частных случаев использован свой набор
вспомогательных переменных, чтобы вывод в объединённой грамматике не мог
перекинуться с одного частного случая на другой (в ходе чего может получиться
недопустимая цепочка). 5. Виды формальных грамматик При более подробном
изучении выразительных возможностей формальных грамматик в связи с
накладываемыми на их правила ограничениями было предложено следующее деление
грамматик (по Н. Хомскому). 5.1. Грамматики общего вида (грамматики
без ограничений или, по Хомскому, грамматики типа 0). Формальный
вид правил грамматик
Иными
словами на их правила не накладывается никаких ограничений, т.е. одна любая
цепочка из смеси знаков основного и вспомогательного алфавита языка (не
нулевой длины) может заменяться на таким же образом составленную другую, в
том числе нулевой длины, т.е. пустую. 5.2. Несокращающие грамматики (или контекстно-зависимые грамматики (КЗГ) или грамматики типа 1). Англоязычное слово
«контекст» (context) в данном случае
переводится как «окружение» (заменяемого знака). Формальный
вид правил грамматик
То
есть ни одно правило не должно сокращать длину цепочки в ходе вывода.
Единственное уточнение связано со случаем, когда формальный язык содержит
пустую цепочку. В этом случае её разрешается породить непосредственно из
аксиомы (начального «Ничто»), причём знак аксиомы не должен встречаться в
правых частях никакого из правил грамматики (когда он уже успел стать
«чем-то»). 5.3. Контекстно-свободные грамматики (КСГ) или грамматики типа
2. Формальный
вид правил грамматик
То
есть в левой части всех правил используется только один вспомогательный знак.
Известна теорема, которая показывает, что использование в левой части правил
только вспомогательных знаков (а не
любого отдельного знака, в т.ч. из основного алфавита языка) не снижает
выразительных возможностей грамматики. Эта теорема приведена, например, в [3]
(гл. 1). 2.4. Праволинейные грамматики (ПГ) или грамматики типа 3. Формальный
вид правил грамматик
То
есть в правой части любого правила может использоваться не более одного
вспомогательного знака, причём если он есть, то он должен стоять справа от
цепочки из основных знаков алфавита. Подобным
образом вводятся и леволинейные
грамматики, обладающие теми же выразительными возможностями:
Задача 1.1. К каким видам относятся грамматики,
рассмотренные нами на предыдущем и этом занятии? Пояснение.
При определения вида грамматики обычно подразумевают ту грамматику, которая
правильно описывает порождение языка и при этом имеет самые жёсткие
ограничения на свои правила. Подобным образом определяют и вид языка (по виду
самой простой, точнее самой ограниченной грамматики, которая его порождает). Задача 1.2. Попробуйте
привести пример, показывающий, что смесь праволинейных и леволинейных правил
в грамматике на деле позволяет строить КС-языки. Задача 1.3. Попробуйте
самостоятельно доказать теорему, упомянутую в п. 5.3. == Ссылки == [1] Ахо А., Ульман Дж. Теория синтаксического
анализа, перевода и компиляции. М.: Мир, Т.1. [2] Хопкрофт Дж., Мотвани Р., Ульман Дж. Введение в теорию
автоматов, языков и вычислений. М.: Вильямс, 2002 (681.3 / X78). (Обложка и оглавление книги). [3] Курочкин В.М., Столяров Л.Н., Сушков Б.Г., Флёров Ю.А. Теория и реализация языков программирования:
Курс лекций. М.: МФТИ, 1978. [4] Шень
А. Программирование:
теоремы и задачи (см. ок. № 118) 2-е изд., М.: МЦНМО, 2004, 296 с. [5] Серебряков В.А. [и др.]. Теория и реализация языков программирования. М.:
МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е изд). – 294 c. (681.3/ Т33). [6] Ахо А., Сети
Р., Ульман Дж. Компиляторы. Принципы, технологии, инструменты. М.; СПб.;
Киев: Вильямс, 2001. (681.3 / А95). (аннотация и
оглавление книги). [7] Мартыненко Б.К. Языки и
трансляции. СПб.: СПбГУ, 2004. (Эльверсия книги в Сети) [8] Фридл Дж. Регулярные выражения. Решения и примеры для
программистов. 2-е изд. М. –[и др.], 2003. [9] Вера
Шабельникова. Превращения кишечной палочки //«Будь
здоров!», 2011, № 9, с. 8-13. |
|
||||
|
|
|
|
||||